Krishna Kannan
Professor
Department of Mechanical Engineering
Krishna Kannan
Research Areas
At the Structures and Solid Mechanics Lab, we focus on developing constitutive theories for materials such as soft tissues, elastomers, and liquid crystal elastomers. These theories are grounded in rigorous mathematics, informed by microstructure and physics, and adhere to thermodynamic principles. We also apply these theories to perform finite element analyses of clinically relevant scenarios.
People
Ph.D Scholars
MS Scholars
Research
Constitutive modelling of soft tissues
Biomechanical modeling is crucial for understanding arterial physiology and pathophysiology, as tissue mechanics significantly influence normal function and the development of vascular diseases. Hence, simple and robust constitutive descriptions of the arterial tissue that describe its quintessential features form the basis for clinically-relevant studies.
1(a). Constitutive modelling of the passive mechanical response of arterial tissues:
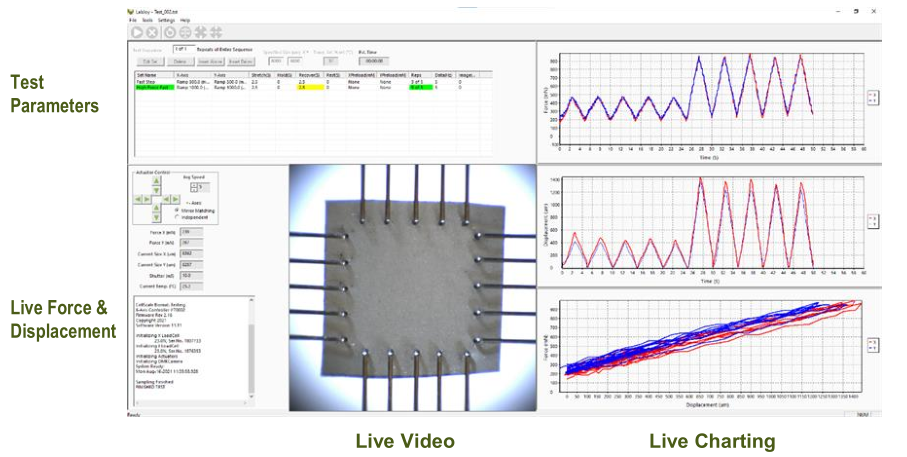
The collagen fibers, which provide mechanical reinforcement to the arterial tissue, are ineffective in supporting compressive loads due to their slender structure. The existing strategy of using a switching criterion to exclude the contribution from compressed fibers in the distribution has the following drawbacks: (i). possibility of discontinuities in the stress, (ii). lack of distinct shear responses in unidirectional composites, and (iii). the fibers could exhibit dual behaviour-simultaneously experiencing tension and compression-depending on the switching criteria.
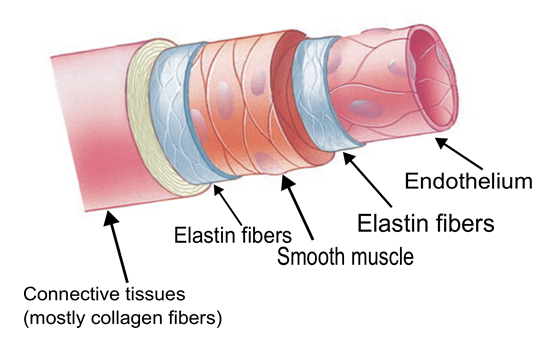
Figure 1. Schematic of the constituents of an artery. (Source- Lauralee Sherwood, 2016)
To address these issues, we propose two classes of vanishing-matched-generalised invariants, based on the Green-Lagrange and Seth-Hill strains. For unidirectional fibers in pure compression, these invariants effectively nullifies fiber contributions, thereby eliminating the need for switching criteria. Additionally, fibers oriented obliquely to the compression direction are modeled to contribute to a varying degree, reflecting their state of combined compression and shear.
Compared to the existing models, both proposed classes demonstrate significantly improved descriptions of planar biaxial data of various healthy and diseased human arterial tissues.
Further, research is ongoing into angular integration (AI)-based switchless constitutive relations for arterial tissues. While AI-based methods demand more computational effort than the generalized structure tensor (GST)-based approach, they excel in capturing the intricate and significant details of fiber orientation.
To model more realistic passive behavior of arteries, the effects of the presence of fluid,
inhomogeneity, and residual stress need to be accounted for.
1(b). Constitutive modelling of the active mechanical response of arterial tissues:
Vascular smooth muscle cells (VSMCs) play a crucial role in regulating arterial function through active contraction, contributing to the maintenance of vasodilation and constriction. Dysfunctional VSMCs are implicated in the pathogenesis of various cardiovascular diseases, including hypertension, atherosclerosis, and vascular calcification.
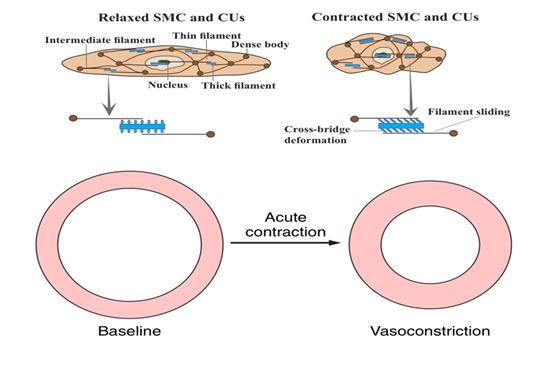
Figure 2. Schematic of contraction of VSMCs. (Source- Lacolley et. al, 2017)
The ability of the VSMCs to contract in response to chemical and mechanical stimuli necessitates chemo-mechanical constitutive relations. The concentration of cytoplasmic Ca2+ regulates the contractile state of VSMCs. In this work, the chemical kinetics, governed by the Hai-Murphy relations, is coupled to the mechanical response in a proper thermodynamic setting. The deformation tensor for the cell contraction is averaged according to the cell dispersion, thereby accounting for the observed level of anisotropy. The framework can emulate observed phenomena, including the presence of an optimal stretch and a crossover stretch limit.
Numerical simulations conducted in ABAQUS® demonstrate the model’s ability to predict uniaxial and biaxial responses of activated arterial strips, showcasing its potential for exploring vascular mechanics under various physiological and pathological conditions.
1(c). Growth & Remodelling (G & R) of arterial tissues:
Growth means an increase in mass achieved locally through increased number or size (hypertrophy) of cells. Remodelling means a change in structure, whether intracellular, cellular, or extracellular. This change is achieved by reorganizing existing constituents such as altering their orientation, cross-linking, or synthesizing new constituents with a different organization. Remodelling may or may not alter the mass density, but it does impact characteristics like stiffness and material symmetry.
Figure 3. Schematic of growth in an abdominal aortic aneurysm. (Source- John Hallett et. al, 2009)
The primary objective of this work is to develop and apply a constraint mixture model that incorporates the mass transport of various constituents from the endothelial layer to gain insights into the underlying mechanisms of arterial remodelling in hypertension. In addition to the conventional stress-mediated description of the growth and remodelling of collagen fibers, we shall also propose a constitutive form for the VSMC-regulated synthesis of collagen fibers that accounts for the current contractile/synthetic phenotype of the VSMCs.
The outcome of this study is a robust G & R model for the arterial wall, and the associated finite element setup for the computation of the evolution of lumen diameter and thickness during the progression of an abdominal aortic aneurysm.
1(d). Constitutive modelling of human brain tissue:
The human brain tissue exhibits a complicated mechanical response to the combined shear and tension/compression loading. In contrast to the conventional approach of deriving the stress tensor from a strain energy potential, we propose an inverse procedure wherein the shear stress is accurately determined based on the mechanical data. The remaining components of the Cauchy stress tensor are systematically determined by using the universal relation, boundary conditions, and the existence of the stored energy. The stored energy constructed using this method can predict the material behaviour accurately for any other mixed modes of deformation. The derived constitutive relation is implemented in ABAQUS® using the UHYPER routine. Further, using ISight®, the material parameters are re-calibrated based on inhomogeneous deformations, thereby yielding parameters more consistent with the actual loading conditions.

Figure 4. Virtual mechanical tests performed on the human brain tissue using ABAQUS®
1(e). Constitutive modelling of the passive response of myocardial tissue:
The heart is a complex organ that relies on the mechanical properties of the myocardium for normal function. The myocardium is a surrounding muscular tissue composed of a network of collagen and muscle fibers that interact to provide the necessary mechanical properties for cardiac function
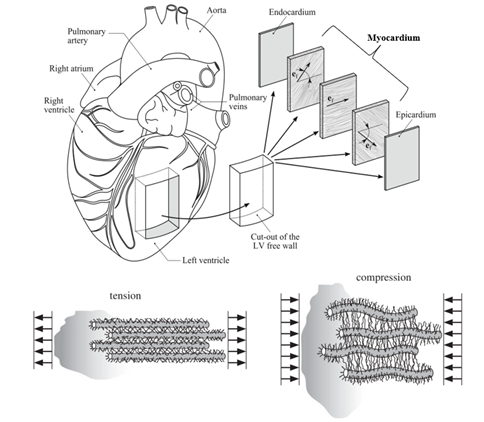
Figure 5. Top- Schematic of the human heart highlighting the myocardium. Bottom- Muscle fibers can sustain some compression, unlike collagen fibers. (Source- Sommer et. al, 2015 & Holzapfel and Ogden, 2009.
To accurately model the anisotropic behavior of the myocardium, it is important to incorporate microstructural information into the constitutive relations. Notwithstanding the dissipative mechanics, the interactions with the surrounding tissue and fluids, the active response, and the growth & remodelling aspects, we take a modest approach and treat the myocardial tissue as an elastic material. Unlike collagen fibers, muscle fibers can withstand some degree of compressive stress due to their relatively large diameter and crosslinking with collagen fibers. The accuracy of the proposed model has important implications for understanding the biomechanics of the heart and developing new treatments for cardiac diseases.
2. Constitutive modelling of liquid crystal elastomers:
Liquid crystal elastomers (LCE) are polymeric materials cross-linked with liquid crystal mesogens. They combine the elastic properties of rubbers and the orientational properties of liquid crystals. This combination results in an entirely new phenomena well beyond what is typically seen in liquid crystals or elastomers. There are different types of LCEs, such as nematic, cholesteric and smectic etc., and they are responsive to various stimuli like temperature, light, electric and magnetic fields. Nematic elastomers are of particular interest, which are LCEs with rod-shaped mesogens whose presence makes the polymer chains stiffer in one direction alone. This causes the chain shape to deviate from the isotropic spherical conformation and acquire a prolate or oblate conformation thereby imparting a transversely isotropic symmetry.
There are theoretical frameworks which treat LCEs as anisotropic Gaussian networks and derive an appropriate stored energy potential as a function of the deformation gradient, as well as the reference and current director fields. This is popularly known as neoclassical theory and has been widely used as a starting point in the constitutive modeling of LCEs. While such an approach is statistically consistent, it does not conform to the axioms of hyperelasticity which mandate that the stored energy does not depend on the current configuration. It would be more rigorous to treat the director kinetics through a viscoelastic model with evolving multiple natural configurations rather than descriptions involving the current director. The goal of this study is to develop a thermodynamically consistent, viscoelastic framework that effectively describes director kinematics in nematic LCEs
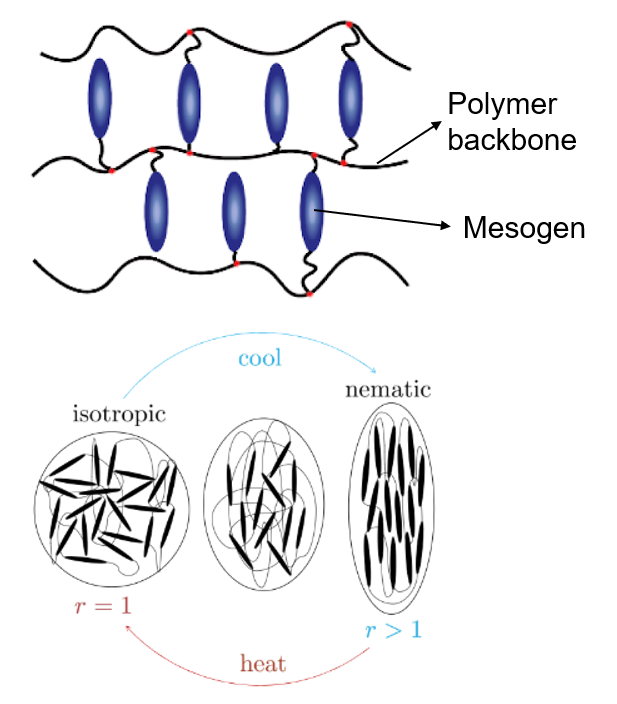
Figure 6. Schematic of the microstructure and mechanics of an LCE (Source- Zhang et. al, 2022).
The collagen fibers, which provide mechanical reinforcement to the arterial tissue, are ineffective in supporting compressive loads due to their slender structure. The existing strategy of using a switching criterion to exclude the contribution from compressed fibers in the distribution has the following drawbacks: (i). possibility of discontinuities in the stress, (ii). lack of distinct shear responses in unidirectional composites, and (iii). the fibers could exhibit dual behaviour-simultaneously experiencing tension and compression-depending on the switching criteria.
Projects
Current projects (2021 – 2024):
- Chemo-mechanical modelling of vascular smooth muscle contraction and 3D numerical analysis of arterial stent angioplasty.
- Semi-analytical inverse procedure-motivated viscoelastic modelling of human brain tissue.
- Angular integration-based switchless constitutive relation for fiber-reinforced soft materials: auto-annihilation of fibers in pure compression.
- Generalised structure tensor-based switchless constitutive relations for arterial tissue: Eliminating all discontinuities in mechanical response.
- Finite element implementation of a novel hyperelastic model for human brain tissue and recalibration of the material parameters based on inhomogenous deformations.
- Viscoelastic framework for modelling nematic liquid crystal polymers.
Future projects:
- 3D numerical analysis of the viscoelastic response of human brain tissue under uniaxial and combined shear deformations.
- Simulation of the mechanics of tumour growth in human brain tissue.
- Simulation of the 3D mechanical response of human heart ventricle during passive inflation.
- A constrained mixture-theoretic and thermodynamic approach to the growth & remodelling of arterial tissues: Application to abdominal aortic aneurysm progression.
- Mode-of-distortion-controlled planar biaxial testing and modelling of soft elastomers.
- Bayesian calibration for uncertainty quantification in switchless constitutive models for arterial tissue.
- Predictions of growth of an abdominal aortic aneurysm by constructing an artificial intelligence-based software built upon physics-based and stochastic continuum models.
Facilities
- High performance workstations for performing computations
- Biaxial Test System- BioTester 5000 (CellScale)
- SAXS (to be procured- a part of CSBM facilities)
Collaboration
- Dr. Seungik Baek, Associate Professor in the Department of Mechanical Engineering, Head of Cardiovascular and Tissue Mechanics Laboratory, Michigan State University,Michigan, USA.
Publications
- A semi-analytical inverse method to obtain the hyperelastic potential using experimental data V Kulwant, K Arvind, D Prasad, P Sreejith, KV Mohankumar, K Kannan Journal of the Mechanics and Physics of Solids 181, 105431 2023
- A new viscoelastic model for human brain tissue using Lode invariants based rate-type thermodynamic framework D Prasad, P Sreejith, K Kannan Applications in Engineering Science 15, 100130 2023
- An efficient mode-of-deformation dependent rate-type constitutive relation for multi-modal cyclic loading of elastomers K Srikanth, P Sreejith, K Arvind, K Kannan, M Pandey International Journal of Plasticity 163, 103517 2023
- A thermodynamic framework for additive manufacturing of crystallizing polymers, Part II: Simulation of the printing of a stent P Sreejith, K Srikanth, K Kannan, KR Rajagopal International Journal of Engineering Science 184, 103790 2023
- A thermodynamic framework for the additive manufacturing of crystallizing polymers. Part I: A theory that accounts for phase change, shrinkage, warpage and residual stress P Sreejith, K Kannan, KR Rajagopal International Journal of Engineering Science 183, 103789 2023
- On the explicit dynamics implementation and validation of partitioned rate-type constitutive relation for dampers K Srikanth, M Pandey, K Kannan Mechanics of Advanced Materials and Structures 30 (2), 284-302 2023
- A new stabilised curvature computation method using the level set function M Sellam, K Kannan, S Natarajan International Journal of Hydromechatronics 6 (4), 325-341 2023
- Switchless constitutive relation for arterial tissues: eliminating all discontinuities in mechanical response. Arvind, K., and K. Kannan. Proceedings of the Royal Society A, 481.2312: 20240634, 2025.
Social Impact
The research undertaken by our group can positively impact healthcare in India and abroad.
The eventual output will be an artificial intelligence-based software based on deep learning guided by data derived from physics-based, stochastic, stress-mediated, continuum level, growth and remodelling solutions together with hard- to-quantify risk factors such as tobacco use and family history, to predict the progression of vascular pathologies.
Based on the developed theory, this software will be undergoing trials in select hospitals, and therefore the medical fraternity will be aware of this tool.
In the long term, this tool is likely to be used by vascular surgeons and cardiologists to get inputs to enable them to make an informed prognosis for both the pre and post-surgical treatment of aneurysms. Such patient-specific computational diagnostic tools will play a greater role in the future and transform medical prognosis, in that more number of lives will be saved by timely interventions.